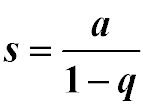‘sichtbarer’ (geometrischer) Beweis der Summe der unendlichen geometrischen Reihe

Dem in Kapitel 05 dargelegten Paradox des Zenon liegt – gemäß unserer Illustration daselbst – die folgende unendliche („geometrische“) Reihe zugrunde:

½ + ¼ + ⅛ +  ...  = 1 [1] 

Geometrische Reihen sind folgendermaßen definiert: Sie setzen sich aus den Folge-Gliedern a, aq, aq², aq³,.. additiv zusammen:

a + aq + aq² + aq³ + ... Entweder für |q|  > 1 (steigende Zahlenfolge der Reihe) oder für q als echter Bruch (fallende Zahlenfolge der Reihe): 0 < q < 1. In unserem Zenon-Beispiel handelt es sich um eine fallende Zahlenfolge der Reihe, denn q = ½ . Das Anfangsglied dieser Reihe ist a = ½ Desweiteren handelt es sich um eine unendliche geometrische Reihe, da für die Summenglieder s_n  gilt: n → ∞   .

Torricelli, ein italienischer Mathematiker und Physiker zur Zeit Galileis, war nicht der erste, welcher unendliche Reihen untersuchte. Die Summe der obigen Reihe wurde schon von Archimedes bestimmt. Aber vermutlich war Torricelli der erste, der die unendliche geometrische Reihe mit positivem q<1 in ihrer Summenbildung verallgemeinert zur Beweisführung brachte. Und zwar findet sich diese zeichnerische Beweisführung dargestellt in seinen „Opera Geometrica“ von 1644. [2] Hischer/Scheid [3], geben in ihrem Buch „Grundbegriffe der Analysis“ eine Rekonstruktion dieser Beweisführung und schreiben zum Schluß dieses Kapitels: “...Mit diesem Ergebnis konnte Torricelli dann den Flächeninhalt eines Parabelsegments berechnen...” [4] .

Hier sind die lateinischen Faksimile der damaligen (umständlichen) Darstellung - für den historisch Interessierten - (kommentarlos) aufgeführt:

Die Methode des Torricelli war demnach (wenn man Hischer/Scheid folgt) eine grundsätzliche und allgemeine Klärung der Summenbildung unendlicher geometrischer Reihen mit positivem q<1. Sie war als erster Anfang zwar genial, aber nicht so elegant, wie sie durch Verbesserung der geometrischen Methodik der Torricellischen Beweisführung inzwischen sich herauskristallisiert hat. Eine sehr schöne, weil sofort einleuchtende solche Beweisführung für positive q<1 findet sich -  ansatzweise dargelegt - bei Lambacher-Schweizer 1968 [5], wie sie im folgenden detailliert dargestellt werden soll.

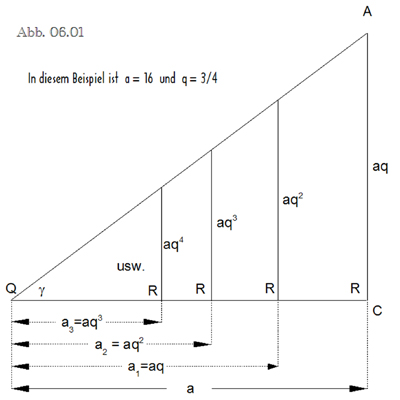
Diese einführende Zeichnung (die sich allerdings bei Lambacher-Schweizer nicht findet) ergibt sich folgendermaßen:

Wenn gemäß des Strahlensatzes (unter der Voraussetzung, daß 0<q<1 gilt) immer das gleiche Streckenverhältnis a : (a^.q) = a_n : (a ^. qⁿ⁺¹) gelten soll, so ergibt sich für die in das große Dreieck QAC hineinverschachtelten kleineren (ähnlichen) Dreiecke mit den unteren Seiten a_i und mit den Winkeln R=90° und γ (= Gamma im gemeinsamen Punkt Q aller dieser Dreiecke):

a / (a^.q) = a₁ / (a ^. q²)   →   a₁= (a ^. a ^. q² ) / (a^.q) =  a^.q

a / (a^.q) = a₂ / (a ^. q³)   →   a₂= (a ^. a ^. q³ ) / (a^.q) =  a^.q²

a / (a^.q) = a₃ / (a ^. q⁴)   →   a₃= (a ^. a ^. q⁴ ) / (a^.q) =  a^.q³

oder allgemein:

a / (a^.q) = a_n / (a ^. qⁿ⁺¹)   →  a_n= (a ^. a ^. qⁿ⁺¹ ) / (a^.q) =  a^.qⁿ

Wenn man jetzt noch der Vollständigkeit halber a₀ = a setzt, so ergibt sich, daß die Terme a, a^.q, a^.q², a^.q³, …, a^.qⁿ …  genau die einzelnen Glieder einer geometrischen Reihenfolge sind (siehe obige Definition), sodaß die Summe dieser Terme die unendliche geometrische Reihe ergibt: s_n = a + a^.q + a^.q² + a^.q³ + …+ a^.qⁿ , sofern für s_n   gilt, n → ∞ .

__________________________________

Es ist also anhand der obigen Zeichnung (Abb. 06.01) die unendliche Folge a, a^.q, a^.q², a^.q³, …, a^.qⁿ … gegeben (Voraussetzung: positives q kleiner 1) und gesucht wird die Summe s dieser Folge s_n = a + a^.q + a^.q² + a^.q³ + …+ a^.qⁿ   (wobei n → ∞) .

Die Behauptung ist:               

Diese Behauptung soll nun bewiesen werden. Als Beweismittel werden einfache geometrische Gesetze (z.B. Strahlensatz, Parallelverschiebung von Strecken) und einfache algebraische Umformungen benutzt.

__________________________________

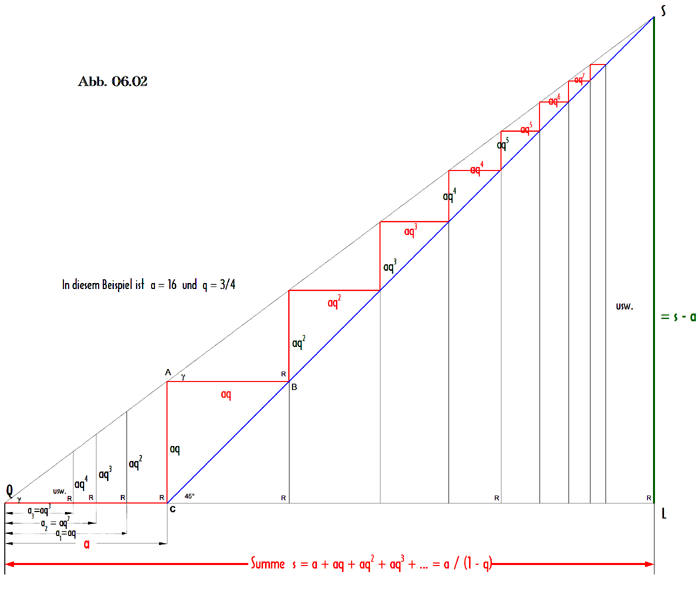
Der entscheidende Beweisdreh liegt nun darin, diese ineinander verschachtelten rechtwinkligen Dreiecke von obiger Abb. 06.01 mit den jeweiligen Katheten a_n und aqⁿ⁺¹ (n=0,1,2,3,...) auseinanderzuziehen und sozusagen außen aneinander zu reihen, um aus der Folge  a₀, a₁, a₂, a₃ ...  die additive Reihe zu machen. D.h. Diese Dreiecke werden per Stufenwinkel γ (Gamma) an der Linie QS sukzessive hintereinander angeordnet (und die jeweilige Dreiecksbasis auf QL parallelverschoben projiziert, um schließlich die Gesamt-Summe s darzustellen):

Daß sich als Ergebnis für die Summe ergibt, soll nun gezeigt werden:

Ist 0 < q < 1, so schneiden sich die schrägen Geraden QAS und CBS im Schnittpunkt S. Die blaue Gerade CBS setzt sich zusammen aus den Diagonalen der Quadrate mit den Seiten aqⁿ (n=1,2,3, ...), die mit wachsendem n immer kleiner werden. Winkel γ (im Punkt Q) ist jedenfalls kleiner als 45°, da aq < a ist. Deswegen schneiden sich die beiden schrägen Geraden QAS und CBS. Es ist für die Ableitung der Summenformel (für die Summe s der unendlichen geometrischen Reihe) selber nicht wichtig, zu wissen, wo genau der Schnittpunkt S liegt. Das Lot von (dem jedenfalls existierenden) S auf die Strecke QCL mit dem Fußpunkt L ergibt die Strecke SL. Sie ist (per parallel verschobener Strecken-Projektion der grün benannten Seiten aqⁿ auf das grüne SL) genau die Summe s (= Strecke QL) minus dem Anfangswert a:   SL = s - a

Die weitere Beweisführung erfolgt durch einfache algebraische Umformung. Zunächst gilt nach Strahlensatz

(s – a) : s = aq : a   →  (s – a)/s  = aq/a   →  (s-a)/s = q  →  sq = s – a  →       s – sq = a   →  s (1 - q) = a     →     

w.z.b.w.

Demnach kann geometrisch gezeigt werden, daß es einen vollkommen eindeutigen äußeren (ganzheitlichen) Rahmen gibt, nämlich das Dreieck mit den Seiten QCS, in das die einzelnen Glieder (d.h. die unendlich vielen Einzelheiten jener treppengestuften kleineren Dreiecke) logisch zwingend hineinverwoben sind. Einzelteile und Ganzheit sind dabei dialektisch und logisch aufeinander bezogen. Die Interessantheit der Beweisführung liegt offenbar darin, daß sich die Summe der unendlichen geometrischen Reihe schließlich aus einfachen Ganzheitsbetrachtungen, die daraus folgen, bestimmen läßt.

[1] „Geometrisch“ heißt solch eine Reihe, weil jedes Glied (außer dem ersten) das „geometrische Mittel“ oder die „mittlere Proportionale“ zwischen den Nachbargliedern ist. So ist beispielsweise ⅛  das geometrische Mittel zu ¼ und 1/16. Denn wenn das gesuchte geom. Mittel von ¼ und 1/16 gleich x ist, so gilt:

¼ : x = x : 1/16  →   ¼ ^. 1/16 = x²    →    x = ½ ^. ¼ = ⅛

Die Definition (endlicher) geometrischer Folgen (d.h. lediglich die Folge-Glieder, abgetrennt durch Komma) und Reihen (d.h. die Glieder sind additiv verbunden) mit Hilfe der mittleren Proportionalen geht auf Euklid zurück. Und zwar jedenfalls im 9. Buch seiner Elemente (Satz 35) - das behaupten Hischer/Scheid, S.79.

[2] und zwar im Kapitel “Quadratura Parabolae”, als Faksimile dargestellt im „Echo Projekt“ zu Torricelli,     S.314 ff. (Siehe die drei Faksimile Abbildungen von Torricelli oben im Text).

[3] Hischer/Scheid S.79-81

[4] Hischer/Scheid S.81

[5] Lambacher-Schweizer, Analysis, S.22